그래프 탐색 알고리즘(BFS,DFS)

그래프 탐색

하나의 정점에서 시작해서 모든 정점을 한번씩 방문하는 작업을 말한다.
그래프 문제들 중 다수는 단순히 정점들의 탐색만으로 해결되기도 한다.

탐색은 정점과 인접한 저점들 중에서 아직 방문하지 않은 정점으로만 가능하다

→ visited등으로 방문한 정점을 관리한다

graph={"A":{"B","C"},
			 "B":{"D"},
			 "C":{"G","H","I"},
			 "D":{"E","F"},
			 "I":{"J"},
}

연결리스트를 이용한 방식을 기준으로 작성했다.

정점의 자식들을 먼저 탐색하는 방식이다.
재귀 혹은 stack을 사용해서 구현한다.
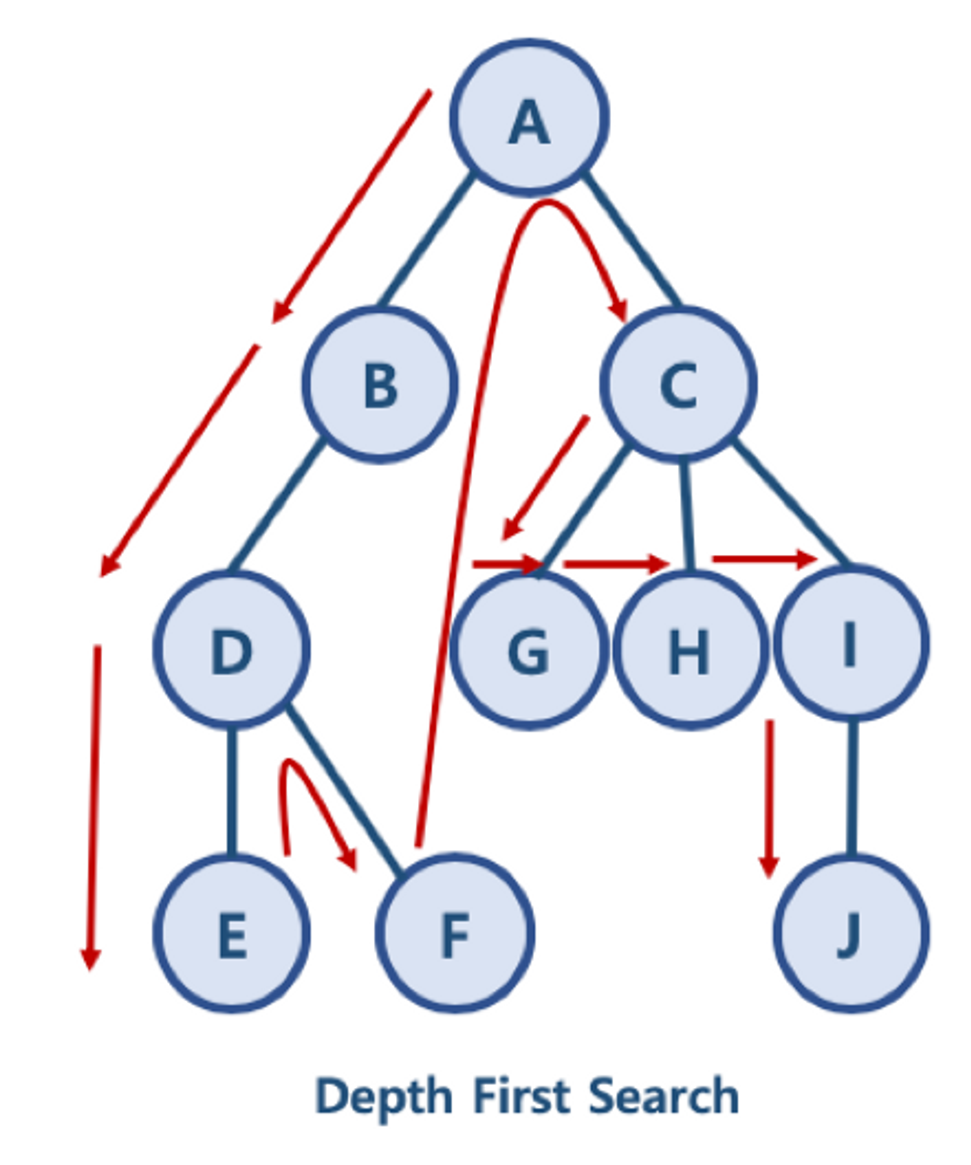
dfs.png|300

재귀를 이용한 구현

def dfs(graph, start, visited,path):
    visited.append(start)
    print(start, end=" ")
    for i in graph[start]:
        if i not in visited:
            dfs(graph, i, visited)

stack을 이용한 구현

def dfs(graph, start, visited):
    stack = [start]
    while stack:
        v = stack.pop()
        if v not in visited:
            visited.append(v)
            stack.extend(graph[v])

시간 복잡도

최대 간선의 수는 v(v-1)가 된다.
⇒ 대부분의 경우에 dfs 인접 리스트의 사용이 인접 행렬보다 시간적으로 유리하다.

queue를 사용해서 구현한다.

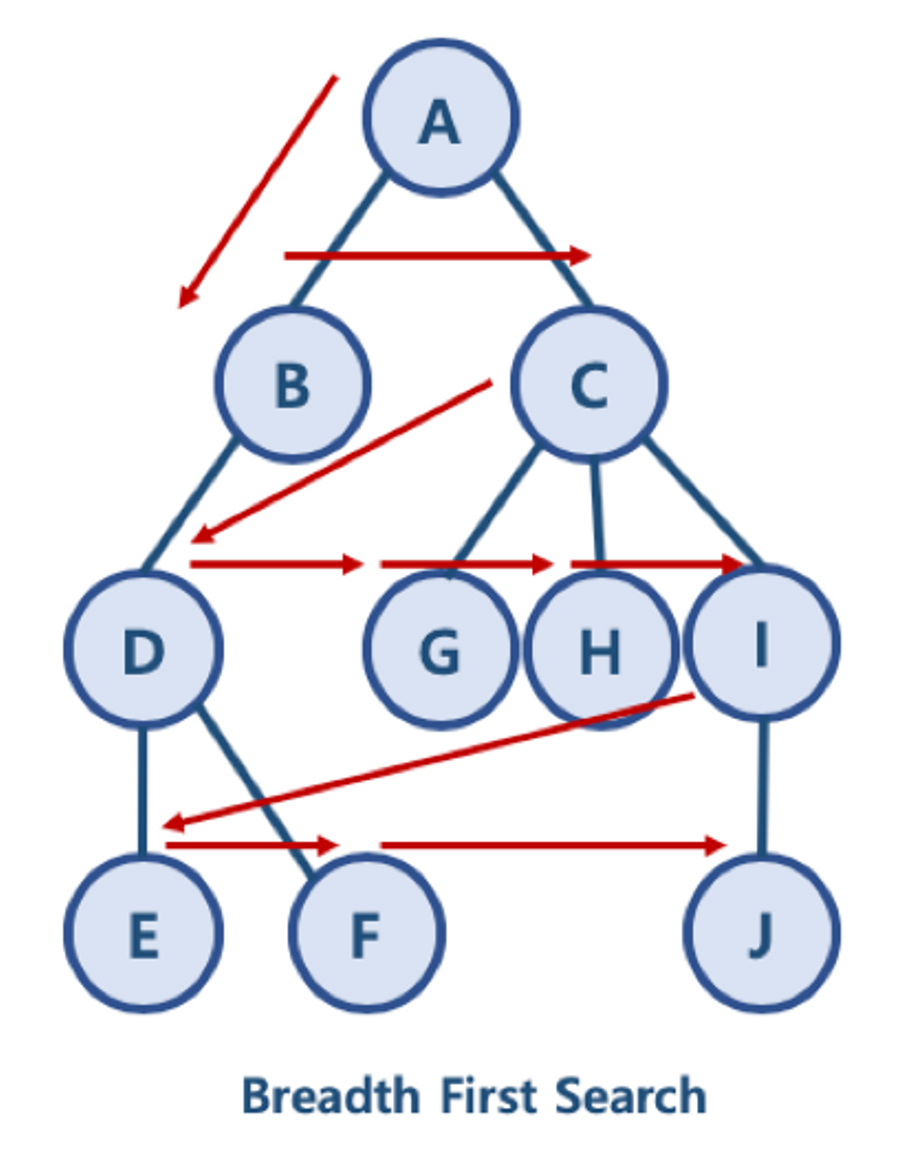
bfs.png|300

def bfs(graph,start,visited):
    queue = [start]
    while queue:
        v = queue.pop(0)
        if v not in visited:
            visited.append(v)
            queue.extend(graph[v])

시간복잡도

bfs와 동일하다.
→ 인접리스트를 사용하는 것이 효율적이다

BFS, DFS 선택 기준

그래프 탐색이 필요한 문제는 DFS와 BFS 모두 이용해서 풀 수 있지만, 어떤 방법을 선택하느냐에 따라서 결과가 좌우되는 문제도 있다.

그러면 어떤 기준으로 BFS 와 DFS 중 한가지 방법을 선택할 수 있을 까?

DFS

BFS